LO
SPAZIO-TEMPO
La fisica moderna ha confermato nel modo più drammatico una delle
idee fondamentali del misticismo orientale: tutti i concetti che usiamo per descrivere la natura sono limitati; non
sono aspetti della realtà, come tendiamo a credere, ma creazioni della mente;
sono parti della mappa, non del territorio. Ogni volta che estendiamo il campo
della nostra esperienza, i limiti della nostra mente razionale diventano
evidenti e siamo costretti a modificare, o persino ad abbandonare, alcuni dei
nostri concetti.
I VECCHI CONCETTI DI SPAZIO E DI TEMPO
Le idee di spazio e
di tempo hanno un posto preminente nella nostra mappa della realtà. Esse servono a ordinare cose ed
eventi nel nostro ambiente e sono quindi di capitale importanza non solo nella
vita quotidiana, ma anche nei nostri tentativi di comprendere la natura
attraverso la scienza e la filosofia. Non c'è legge della fisica che per la sua
formulazione non richieda l'uso dei concetti di spazio e di tempo. La profonda modificazione di questi concetti
fondamentali determinata dalla teoria della relatività fu perciò una delle più
grandi rivoluzioni nella storia della scienza.
La fisica classica era basata sull'idea sia di uno spazio assoluto, tridimensionale, indipendente
dagli oggetti materiali in esso contenuti e regolato dalle leggi della
geometria euclidea, sia di un tempo inteso come dimensione separata, anch'esso assoluto,
che scorre uniformemente e indipendentemente dal mondo materiale. In
Occidente, questi concetti di spazio e di tempo erano così profondamente
radicati nella mente di filosofi e scienziati che furono assunti come proprietà
vere e indiscusse della natura.
La geometria
La convinzione che la geometria, più che far parte della struttura
che usiamo per descrivere la natura, sia inerente a questa ha le sue origini
nel pensiero greco. La geometria assiomatica era l'aspetto principale della
matematica greca ed ebbe una profonda influenza sulla filosofia greca. Il suo
metodo, che consisteva nel partire da assiomi indiscussi per ricavarne dei
teoremi mediante il ragionamento deduttivo, divenne caratteristico del pensiero
filosofico greco; la geometria fu perciò al centro di tutte le attività
intellettuali e costituì la base dell'educazione filosofica. Si dice che la
porta dell'Accademia di Platone in Atene recasse la scritta «Non entri chi non
conosce la geometria». I Greci ritenevano che i loro teoremi matematici fossero
espressioni di verità eterne ed esatte riguardanti il mondo reale, e che le forme
geometriche fossero manifestazioni della bellezza assoluta. La geometria era
considerata la combinazione perfetta della logica e della bellezza e pertanto
era ritenuta di origine divina. Di qui il detto di Platone, «il dio è
geometra».
Poiché la geometria era vista come la rivelazione del dio, era
ovvio per i Greci ritenere che i cieli dovessero avere forme geometriche
perfette; ciò volle dire che i corpi celesti dovevano muoversi su orbite
circolari. Per presentare il quadro in modo ancor più geometrico si pensò che i
corpi celesti fossero fissati a una serie di sfere cristalline concentriche che
si muovevano come un tutto unico, con
Nei secoli successivi, la geometria greca continuò a esercitare una
forte influenza sulla filosofia e sulla scienza dell'Occidente. Gli
Elementi di Euclide furono il libro di testo classico nelle scuole
europee fino all'inizio di questo secolo, e la geometria euclidea
venne considerata la vera natura dello spazio per più di duemila anni. Fu
necessaria l'opera di Einstein perché scienziati e
filosofi si rendessero conto che la
geometria non è inerente alla natura, ma è imposta a essa dalla nostra mente.
Dice Henry Margenau:
«Al centro della teoria della relatività c'è il riconoscimento che
la geometria... è una costruzione dell'intelletto. Solo accettando questa
scoperta, la mente può sentirsi libera di modificare le nozioni tradizionali di
spazio e di tempo, di riesaminare tutte le possibilità utilizzabili per
definirle, e di scegliere quella formulazione che più concorda con
l'esperienza».
SPAZIO E TEMPO PER
LA FILOSOFIA ORIENTALE
La filosofia
orientale, a differenza di quella greca, ha sempre sostenuto che lo spazio e il
tempo sono costruzioni della mente. I mistici orientali consideravano questi concetti - come tutti gli altri concetti intellettuali
- relativi, limitati e illusori. In un
testo buddhista, per esempio, troviamo le seguenti
parole:
«Il Buddha insegnava, o monaci, che... il
passato, il futuro, lo spazio fisico,... e le singole cose non fossero che
nomi, forme di pensiero, parole di uso comune, realtà puramente superficiali».
Quindi, nell'Estremo Oriente la geometria non raggiunse mai la
considerazione di cui godeva nell'antica Grecia, sebbene ciò non significhi che
gli Indiani e i Cinesi ne avessero una scarsa conoscenza. Essi se ne servivano
ampiamente per costruire altari di precise forme geometriche, per misurare i
terreni e per tracciare le mappe celesti, ma mai per determinare verità
astratte ed eterne. Questo atteggiamento filosofico si riflette anche nel fatto
che l'antica scienza orientale generalmente non ritenne necessario far
rientrare la natura in uno schema geometrico di linee rette e di cerchi
perfetti. A tale proposito, le osservazioni di Joseph
Needham sull'astronomia cinese sono molto
interessanti:
«Gli [astronomi] cinesi non sentirono la necessità di forme
[geometriche] di spiegazione: gli esseri che costituivano l'organismo
universale seguivano il loroT ao
ciascuno secondo la propria natura, e i loro movimenti avrebbero potuto essere
trattati nella forma essenzialmente "non rappresentativa"
dell'algebra. I Cinesi furono quindi liberi dall'ossessione degli astronomi
europei per il cerchio inteso come la più perfetta delle figure, ... né fecero
l'esperienza dello stretto vincolo medioevale delle sfere cristalline».
Gli antichi scienziati e filosofi orientali possedevano già
l'atteggiamento, tanto fondamentale per la teoria della relatività, secondo il
quale le nostre nozioni di geometria non sono proprietà assolute e immutabili
della natura, bensì costruzioni intellettuali.
Secondo le parole di Aśvaghosa,
«Sia chiaro che lo spazio non è altro che un modo di particolarizzazione che non ha esistenza reale di per se
stesso... Lo spazio esiste solo in relazione alla nostra coscienza che particolarizza».
Queste stesse considerazioni valgono per la nostra idea di tempo. I
mistici orientali collegano entrambe le nozioni di spazio e di tempo a
particolari stati di coscienza. Essendo in grado, mediante la meditazione, di
oltrepassare lo stato ordinario, essi si
sono resi conto che i concetti convenzionali di spazio e di tempo non sono la
verità ultima. La loro esperienza mistica porta a concetti di spazio e
tempo più raffinati, che per molti aspetti somigliano a quelli della fisica
moderna così come sono presentati dalla teoria della relatività.
NUOVA CONCEZIONE SPAZIO E TEMPO
Qual è, dunque, questa nuova concezione dello spazio e del tempo
che emerge dalla teoria della relatività? Essa si basa sulla scoperta che tutte le misure di spazio e tempo sono
relative. Ovviamente, la relatività delle specificazioni spaziali non
costituiva nulla di nuovo. Si sapeva bene prima di Einstein
che la posizione di un oggetto nello spazio può essere definita solo rispetto a
qualche altro oggetto. Di solito, ciò viene fatto servendosi di tre coordinate
e il punto dal quale si misurano le coordinate può essere chiamato la posizione dell'«osservatore».
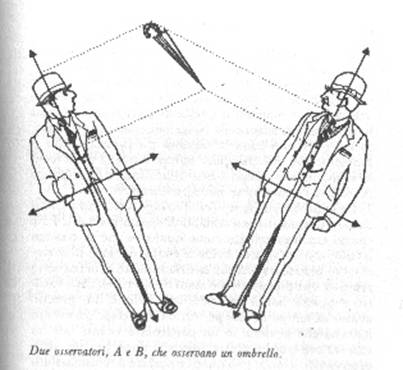
Due
osservatori A e B che osservano un ombrello
Perché la relatività di tali coordinate risulti chiara, immaginiamo
due osservatori che galleggiano nello spazio e che osservano un ombrello, come
nel disegno. L'osservatore A vede l'ombrello alla sua sinistra e leggermente
inclinato, cosicché l'estremo superiore è un po' più vicino a lui.
L'osservatore B , viceversa, vede l'ombrello alla sua destra inclinato in modo
tale che l'estremità superiore risulta più distante. Estendendo questo esempio
bidimensionale alle tre dimensioni, diventa chiaro che tutte le specificazioni
spaziali - quali, «sinistra», «destra»,
«sopra», «sotto», obliquo», ecc. –
dipendono dalla posizione dell'osservatore e sono quindi relative. Ciò
era noto molto prima della teoria della relatività. Per quanto riguarda il
tempo, tuttavia, la situazione nella fisica classica era completamente
differente. Si supponeva infatti che
l'ordine temporale tra due eventi fosse indipendente da qualsiasi osservatore,
e alle specificazioni che si riferivano al tempo - quali, «prima», «dopo», o
«simultaneamente» - veniva dato un significato
assoluto, indipendente da qualsiasi sistema di coordinate.
Einstein riconobbe che anche le
specificazioni temporali sono relative e dipendono dall'osservatore. Nella vita
quotidiana, l'impressione di poter ordinare gli eventi attorno a noi in
un'unica sequenza temporale è creata dal fatto che la velocità della luce -
1.
Per ottenere questo risultato è essenziale tener conto del fatto che la
velocità della luce è la stessa per tutti gli osservatori.
Due eventi che un osservatore vede come simultanei possono avvenire
in diverse sequenze temporali per altri osservatori. A velocità ordinarie, le
differenze sono talmente piccole che non possono essere rivelate, ma quando le
velocità si avvicinano a quella della luce, esse danno luogo ad effetti
misurabili. Nella fisica delle alte energie, in cui gli eventi sono interazioni
tra particelle che si muovono con velocità quasi uguale a quella della luce, la
relatività del tempo è ben dimostrata e ha ricevuto conferma da innumerevoli
esperimenti. [2]
2. Si noti che in questo caso l'osservatore è
in quiete nel suo laboratorio, ma gli eventi che egli osserva sono prodotti da
particelle che si muovono con velocità differenti. L'effetto è lo stesso. Ciò che
conta è il moto relativo tra l'osservatore e gli eventi osservati, mentre è
irrilevante quale dei due si muove rispetto al laboratorio.
La relatività del tempo ci costringe anche ad abbandonare il concetto newtoniano di spazio
assoluto. Tale spazio era immaginato come qualcosa che in ciascun istante
conteneva una definita configurazione di materia; ora però si è visto che la
simultaneità è un concetto relativo, che dipende dallo stato di moto
dell'osservatore, e quindi non è più possibile definire un preciso istante di
tempo uguale per tutto l'universo. Un evento lontano che avviene in un
particolare istante per un osservatore può avvenire prima o dopo per un altro
osservatore. Non si può dunque parlare in senso assoluto dell'«universo in un
dato istante»: non esiste uno spazio assoluto indipendente dall'osservatore.
La teoria della
relatività ha quindi dimostrato che tutte le misure che implicano spazio e
tempo perdono il loro significato assoluto e ci ha costretti ad abbandonare i
concetti classici di spazio e tempo assoluti. L'importanza fondamentale di questa evoluzione è
stata espressa chiaramente da Mendel Sachs con le seguenti parole:
«L'effettiva rivoluzione avvenuta con la teoria di Einstein... fu l'abbandono dell'idea secondo la quale il
sistema di coordinate spazio-temporali ha un significato obiettivo come entità
fisica indipendente. Al posto di questa idea, la teoria della relatività
suggerisce che le coordinate spazio e tempo sono soltanto elementi di un
linguaggio che viene usato da un osservatore per descrivere il suo ambiente».
Questa affermazione di un fisico contemporaneo mostra la stretta
affinità che c'è tra le nozioni di spazio e di tempo nella fisica moderna e
quelle dei mistici orientali, i quali sostengono, con parole già da noi citate,
che spazio e tempo «non sono altro che nomi, forme di pensiero, parole di uso
comune».
Poiché spazio e tempo sono ora ridotti al ruolo soggettivo di
elementi del linguaggio usato da un particolare osservatore per descrivere i
fenomeni naturali dal suo punto di vista, ciascun osservatore descriverà quei
fenomeni in modo diverso. Per astrarre alcune leggi naturali universali dalle
loro descrizioni, gli osservatori devono formulare queste leggi in modo tale
che esse abbiano la stessa forma in tutti i sistemi di coordinate, cioè per
tutti gli osservatori, qualunque sia la loro posizione e il loro moto relativo.
Questa condizione è nota come principio
di relatività ed è stata, in effetti, il punto di partenza della teoria omonima.
È interessante notare come questa teoria fosse già contenuta in forma
embrionale in un paradosso che si presentò ad Einstein
all'età di soli sedici anni. Egli provò a immaginare come sarebbe apparso un
fascio di luce a un osservatore che viaggiasse insieme con esso alla stessa
velocità, e concluse che tale osservatore avrebbe visto il fascio di luce come
un campo elettromagnetico che oscillava su e giù senza propagarsi, cioè senza
formare un'onda. Tuttavia, in fisica non si conosce un tale campo
elettromagnetico. Il giovane Einstein pensò allora
che, se era così, la stessa cosa che a un osservatore appariva come un ben noto
fenomeno elettromagnetico, cioè un'onda luminosa, a un altro osservatore
sarebbe apparsa come un fenomeno che contraddiceva le leggi della fisica, e
questo non gli sembrò possibile.
Negli anni successivi, Einstein capì che
il principio di relatività può essere soddisfatto, nella descrizione dei
fenomeni elettromagnetici, solo se tutte le specificazioni, non solo spaziali
ma anche e temporali, sono relative.
Le leggi della
meccanica, che governano i fenomeni associati ai corpi in movimento, e le leggi
dell'elettrodinamica, la teoria dell'elettricità e del magnetismo, possono
allora essere formulate in uno schema «relativistico» comune che, insieme con
le tre coordinate spaziali, incorpori il tempo come quarta coordinata che deve
essere specificata rispetto all'osservatore.
Per verificare se il principio di relatività è soddisfatto, cioè se
le equazioni di una certa teoria appaiono le stesse in tutti i sistemi di
coordinate, si deve naturalmente essere in grado di tradurre le specificazioni
spazio-temporali da un sistema di coordinate, o «sistema di riferimento»,
all'altro.
Tali traduzioni, o «trasformazioni», come vengono chiamate, erano
già ben note e ampiamente usate nella fisica classica. Per esempio, la
trasformazione tra i due sistemi di riferimento rappresentati a pag. 191
esprime ciascuna delle due coordinate dell'osservatore A (una orizzontale e
altra verticale, indicate nel disegno dalle linee orientate che si intersecano)
come combinazione delle coordinate dell'osservatore B, e viceversa. Le
espressioni esatte possono essere ricavate facilmente con l'aiuto della
geometria elementare.
Nella fisica
relativistica, si presenta una situazione nuova, perché alle tre coordinate
spaziali si aggiunge il tempo come quarta dimensione. Poiché le trasformazioni
tra differenti sistemi di riferimento esprimono ciascuna coordinata di un
sistema come combinazione delle coordinate dell'altro, in generale una coordinata
spaziale in un sistema apparirà, in un altro sistema, come combinazione sia
delle coordinate spaziali sia di quella temporale. Siamo in presenza di una
situazione completamente nuova. Ogni variazione del sistema di coordinate
ricombina spazio e tempo in un modo matematicamente ben definito. Pertanto i
due concetti non possono più essere separati, poiché ciò che è spazio per un
osservatore sarà combinazione di spazio e tempo per l'altro. La teoria della relatività ha dimostrato
che lo spazio non è tridimensionale e il tempo non è una entità separata.
Entrambi sono profondamente e inseparabilmente connessi e formano un continuo quadridimensionale chiamato
«spazio-tempo». Questo concetto di spazio-tempo fu introdotto da Hermann Minkowski in una famosa conferenza
del 1908 con le seguenti parole:
«Le concezioni di spazio e tempo che desidero esporvi sono sorte
dal terreno della fisica sperimentale, e in ciò sta la loro forza. Esse sono
fondamentali. D'ora in poi lo spazio di per se stesso e il tempo di per se
stesso sono condannati a svanire in pure ombre, e solo una specie di unione tra
i due concetti conserverà una realtà indipendente».
I concetti di
spazio e tempo sono talmente fondamentali per la descrizione dei fenomeni
naturali che la loro modificazione comporta un cambiamento dell'intero schema
teorico di cui ci serviamo in fisica per descrivere la natura. Nel nuovo schema, spazio e tempo
sono trattati sullo stesso piano e sono connessi in modo inseparabile: nella
fisica relativistica non possiamo mai parlare di spazio senza parlare di tempo,
e viceversa. Ogni volta che ci si occupa di fenomeni che comportano elevate
velocità, si deve usare questo nuovo schema di interpretazione.
Il legame profondo che esiste tra spazio e tempo era ben noto in
astronomia, in un contesto diverso, molto prima della teoria della relatività.
Gli astronomi e gli astrofisici hanno a che fare con
distanze estremamente grandi e di nuovo, in questo caso, diventa importante il
fatto che la luce impieghi un certo intervallo di tempo per andare dall'oggetto
osservato all'osservatore. Poiché la velocità della luce è finita, gli
astronomi non osservano mai l'universo nel suo stato attuale, ma guardano
sempre indietro, nel passato. Per andare dal Sole alla Terra, la luce impiega otto
minuti, e quindi, in ogni momento, noi vediamo il Sole come era otto minuti
prima. Analogamente, vediamo la stella più vicina come essa era quattro anni
fa, e con i nostri potenti telescopi possiamo vedere le galassie come erano
milioni di anni fa.
Il fatto che la velocità della luce è finita non rappresenta in
alcun modo un problema per gli astronomi, anzi costituisce un grande vantaggio.
Permette loro di osservare tutte le fasi dell'evoluzione di stelle, ammassi
stellari o galassie guardando semplicemente nello spazio e indietro nel tempo.
Tutti i tipi di fenomeni che sono avvenuti nei milioni di anni del passato
possono effettivamente essere osservati in qualche punto del cielo. Gli
astronomi sono quindi abituati a riconoscere l'importanza del legame che esiste
tra spazio e tempo. Quello che la teoria della relatività ci dice di nuovo è
che questo legame è importante non solo quando abbiamo a che fare con grandi
distanze, ma anche quando abbiamo a che fare con grandi velocità. Persino qui
sulla Terra la misura di una distanza non è indipendente dal tempo, perché essa
richiede la specificazione dello stato di moto dell'osservatore, e quindi un
riferimento al tempo.
FUNZIONE UNIFICATRICE
L'unificazione dello spazio e del tempo comporta - come è già stato
detto nel capitolo precedente - una
unificazione di altri concetti fondamentali, e questa funzione unificatrice è
l'aspetto più caratteristico della struttura della relatività. Concetti che
nella fisica non relativistica sembravano del tutto privi di qualsiasi
relazione, ora sono considerati semplicemente aspetti diversi di un medesimo
concetto. La sua funzione unificatrice conferisce alla struttura della
relatività una grande eleganza e una profonda bellezza dal punto di vista
matematico. Molti anni di lavoro con la teoria della relatività ci hanno
portato ad apprezzare questa eleganza e a impadronirci perfettamente del suo
formalismo matematico; tuttavia ciò è stato di scarso aiuto per la nostra
intuizione. Non abbiamo alcuna esperienza sensoriale diretta dello spazio-tempo
quadridimensionale né degli altri concetti relativistici. Ogni volta che
studiamo dei fenomeni naturali che comportano alte velocità, ci risulta molto
difficile trattare questi concetti sia a livello di intuizione sia a livello di
linguaggio ordinario.
Per esempio, nella fisica classica si è sempre dato per scontato
che un regolo ha la stessa lunghezza in moto o in quiete. La teoria della
relatività ha mostrato che ciò non è vero. La
lunghezza di un oggetto dipende dal suo moto rispetto all'osservatore e cambia
con la velocità di quel moto. La variazione è tale che l'oggetto si contrae
nella direzione del moto. La lunghezza del regolo è massima in un sistema di
riferimento nel quale esso è in quiete e diminuisce col crescere della velocità
rispetto all'osservatore. Durante gli esperimenti di «diffusione» della fisica
delle alte energie, in cui le particelle si urtano a grandissime velocità, la
contrazione relativistica raggiunge valori così elevati che particelle di forma
sferica vengono schiacciate fino ad assumere la forma di «frittelle». È importante comprendere che non ha alcun
senso chiedersi quale sia la lunghezza
«reale» di un oggetto, proprio come nella vita quotidiana non ha senso
chiedersi quale sia la lunghezza reale dell'ombra di una persona. L'ombra è
la proiezione su un piano bidimensionale di un insieme di punti dello spazio
tridimensionale e la sua lunghezza è diversa a seconda dell'angolo di
proiezione. Analogamente, la lunghezza di un oggetto in moto è la proiezione,
su uno spazio tridimensionale, di un insieme di punti dello spazio-tempo
quadridimensionale; essa è diversa in sistemi di riferimento diversi.
GLI INTERVALLI DI TEMPO
Ciò che è vero per
le lunghezze, è vero anche per gli intervalli di tempo. Anch'essi dipendono dal
sistema di riferimento, ma al contrario delle distanze spaziali diventano tanto
più lunghi quanto più aumenta la velocità rispetto all'osservatore. Ciò significa che gli orologi in
moto rallentano e il tempo scorre più lentamente. Questi orologi possono essere
di tipi svariati: orologi meccanici, orologi atomici, o addirittura il battito
del cuore dell'uomo. Se di una coppia di gemelli uno dei due partisse per un
veloce viaggio di andata e ritorno nello spazio esterno, al suo rientro a casa
risulterebbe più giovane del fratello, perché dal punto di vista di quest'ultimo, rimasto a terra, tutti i suoi «orologi» - il
battito del cuore, il flusso del sangue, le onde cerebrali, ecc. - sarebbero
rallentati durante il viaggio. Il viaggiatore, naturalmente, non si
accorgerebbe di alcunché di insolito, ma al suo ritorno si renderebbe
improvvisamente conto che ora il fratello gemello è molto più vecchio. Questo «paradosso dei gemelli» è forse il
più famoso paradosso della fisica moderna. Esso ha provocato accese
discussioni nelle riviste scientifiche, ancora non completamente sopite: una
prova eloquente del fatto che la realtà
descritta dalla teoria della relatività non può essere afferrata facilmente
dalla nostra intelligenza ordinaria.
Il rallentamento degli orologi in moto, per quanto possa sembrare
incredibile, è facilmente sottoposto a verifica nella fisica delle particelle.
La maggior parte delle particelle subatomiche sono instabili, cioè dopo un
certo periodo di tempo si disintegrano in altre particelle. Numerosi
esperimenti hanno confermato il fatto che la vita media [3] di una di queste
particelle instabili dipende dal suo stato di moto e aumenta con la sua
velocità.
3. Forse è bene fare una piccola
precisazione tecnica. Quando parliamo della vita di un determinato tipo di
particella instabile, intendiamo sempre la vita media. A causa del carattere
statistico della fisica subatomica. non possiamo fare alcuna affermazione
precisa sulle singole particelle.
Particelle che si muovono
con una velocità pari all'80 per cento di quella della luce vivono circa l,7
volte di più delle loro «gemelle» lente, mentre con una velocità pari al 99 per
cento della velocità della luce vivono circa 7 volte più a lungo. Anche in
questo caso ciò non significa che cambia la vita media reale della particella.
Dal punto di vista della particella, la sua vita media è sempre la stessa, ma
dal punto di vista dell'osservatore nel laboratorio l'«orologio interno» della
particella ha rallentato e perciò essa vive più a lungo.
Tutti questi
effetti relativistici sembrano strani soltanto perché con i nostri sensi non
possiamo fare alcuna esperienza diretta del mondo quadridimensionale dello
spazio-tempo, ma possiamo osservarne soltanto le «immagini» tridimensionali. Queste immagini hanno aspetti
diversi in diversi sistemi di riferimento; oggetti in moto appaiono diversi da
oggetti fermi e orologi in moto scandiscono il tempo con ritmo diverso. Questi
effetti possono sembrare paradossali se non comprendiamo che essi sono soltanto
le proiezioni di fenomeni quadridimensionali, proprio come le ombre sono
proiezioni di oggetti tridimensionali. Se potessimo visualizzare la realtà
dello spazio-tempo quadridimensionale, non ci sarebbe nulla di paradossale.
L’ESPRIENZA PLURIDIMENSIONALE
I mistici
orientali, come è stato detto sopra, sembrano in grado di raggiungere stati di
coscienza non ordinari, nei quali trascendono il mondo tridimensionale della
vita quotidiana per provare l'esperienza di una realtà superiore,
pluridimensionale. Aurobindo per esempio parla di «un
mutamento sottile che fa sì che la vista veda in una specie di quarta
dimensione». Le dimensioni di questi stati di coscienza non sono forse le
stesse con le quali abbiamo a che fare nella fisica relativistica, ma è
sorprendente il fatto che esse abbiano condotto i mistici a nozioni di spazio e
tempo che sono molto simili a quelle della teoria della relatività.
In tutto il misticismo orientale sembra essere presente una profonda intuizione del carattere
«spazio-temporale» della realtà. Viene ribadito con insistenza che spazio e
tempo sono uniti in maniera inseparabile, un fatto questo peculiare della
fisica relativistica. Questa nozione intuitiva di spazio e tempo ha trovato,
forse, la sua esposizione più chiara e la sua elaborazione di più vasta portata
nel Buddhismo, e in particolare nella scuola Avatamsaka del buddhismo Mahāyāna.
L'Avatamsaka-sūtra, sul quale si
basa tale scuola, fornisce una viva
descrizione dell'esperienza che si ha del mondo nello stato di
illuminazione. La consapevolezza di una «compenetrazione di spazio e tempo»
- un'espressione perfetta per descrivere lo spazio-tempo è ripetutamente
sottolineata nel Sūtra ed è vista come una
caratteristica essenziale dello stato di illuminazione della mente.
Per usare le parole di D.T. Suzuki:
«Il significato dell'Avatamsaka e della
sua filosofia è incomprensibile a meno di non provare una volta... uno stato di
totale dissolvimento in cui non c'è più distinzione tra mente e corpo, soggetto
e oggetto... Ci guardiamo intorno e sentiamo che... ogni oggetto è connesso con
ogni altro oggetto... non solo spazialmente, ma temporalmente. ... Come realtà di pura esperienza, non c'è
spazio senza tempo, non c'è tempo senza spazio; essi si compenetrano».
Difficilmente si potrebbe trovare un modo migliore per descrivere
il concetto relativistico di spazio-tempo. Confrontando la citazione di Suzuki con quella, riportata precedentemente, di Minkowski, è interessante anche notare che sia il fisico
sia il buddhista sottolineano il fatto che le loro
concezioni di spazio-tempo sono basate sull'esperienza: in un caso su
esperimenti scientifici, nell'altro sull'esperienza mistica.
A parer mio, la
particolare disposizione dell'intuito dei mistici orientali a dare importanza
al concetto di tempo è una delle ragioni principali per cui, in genere, le loro
idee sulla natura sembrano corrispondere molto più da vicino alle concezioni
scientifiche moderne di quanto non facciano quelle della maggior parte dei
filosofi greci.
La filosofia della natura dei Greci era, nel suo insieme, essenzialmente
statica e in buona parte si basava su considerazioni geometriche. Si potrebbe
dire che era estremamente «non-relativistica», e la sua profonda influenza sul
pensiero occidentale può essere certamente uno dei motivi per cui noi abbiamo
difficoltà concettuali tanto grandi di fronte ai modelli relativistici della
fisica moderna. Le filosofie orientali, viceversa, sono filosofie dello
«spazio-tempo» e quindi la loro intuizione spesso si avvicina moltissimo alle
concezioni della natura suggerite dalle nostre moderne teorie relativistiche.
Essendo basate sulla consapevolezza che spazio e tempo sono
intimamente connessi e compenetrati, le concezioni del mondo della fisica
moderna e del misticismo orientale sono entrambe intrinsecamente dinamiche e
contengono il tempo e il mutamento come propri elementi essenziali. Questo
punto sarà esaminato dettagliatamente nel prossimo capitolo, e costituisce il
secondo tema importante, a cui si farà costante riferimento nel nostro
confronto tra fisica e misticismo orientale (il primo è quello dell'unità di
tutte le cose e di tutti gli eventi). Studiando i modelli relativistici e le
teorie della fisica moderna, vedremo che ognuno di essi è una straordinaria
esemplificazione dei due elementi basilari della concezione orientale del
mondo: l'unicità fondamentale
dell'universo e il suo carattere intrinsecamente dinamico.
La teoria della relatività, nella forma esaminata finora, è nota
come «teoria speciale della relatività». Essa fornisce uno schema che vale per
la descrizione tanto dei fenomeni associati ai corpi in moto, quanto di quelli
associati all'elettricità e al magnetismo; gli elementi caratteristici
fondamentali di questo schema sono la relatività dello spazio e del tempo e la
loro unificazione in uno spazio-tempo quadridimensionale.
Nella «teoria generale della relatività», lo schema della teoria
speciale è stato esteso fino a includere la gravità. L'effetto della gravità,
secondo la relatività generale, è di curvare lo spazio-tempo. Di nuovo, questo
fatto è estremamente difficile da visualizzare. Possiamo facilmente immaginare
una superficie curva bidimensionale, come per esempio il guscio di un uovo,
perché vediamo una superficie curva del genere nello spazio tridimensionale. Il
significato del termine curvatura per superfici curve bidimensionali è quindi
del tutto chiaro; ma quando si trasferisce questo concetto allo spazio
tridimensionale - per non parlare dello spazio-tempo quadridimensionale - la
nostra immaginazione ci abbandona. Poiché non possiamo guardare lo spazio
tridimensionale «dall'esterno», non riusciamo a immaginare come possa essere
«curvato in qualche direzione».
Per comprendere il significato dello spazio-tempo curvo, dobbiamo
servirci, come analogie, di superfici curve bidimensionali. Immaginiamo, per
esempio, la superficie di una sfera. Il fatto decisivo che rende possibile
l'analogia con lo spazio-tempo è che la curvatura è una proprietà intrinseca
alla superficie e può essere misurata senza uscire nello spazio
tridimensionale. Un insetto bidimensionale, confinato sulla superficie della
sfera e incapace di percepire lo spazio tridimensionale, potrebbe lo stesso
scoprire che la superficie sulla quale vive è curva, purché sia in grado di
eseguire misurazioni geometriche.
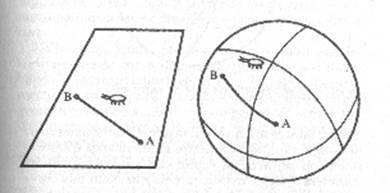
Come
si traccia una linea retta su un piano e su una sfera
Per capire come questo possa avvenire, dobbiamo confrontare la
geometria del nostro insetto sulla sfera con quella di un altro insetto simile
che viva su una superficie piana. Supponiamo che i due insetti comincino il
loro studio della geometria tracciando una linea retta, definita come il
percorso più breve tra due punti. Il risultato è indicato nella figura. Vediamo
che l'insetto sulla superficie piana ha disegnato una vera e propria linea
retta, ma cosa ha fatto l'insetto sulla sfera? Per lui, la linea che ha
disegnato è la più breve tra quelle che uniscono i punti A e B, poiché
qualsiasi altra linea che può tracciare risulterebbe più lunga; ma noi, dal
nostro punto di vista, ci accorgiamo che questa linea è una curva (per la
precisione, si tratta di un arco di cerchio massimo). Supponiamo ora che i due
insetti studino i triangoli. L'insetto sul piano troverà che la somma dei tre
angoli di qualsiasi triangolo è uguale a due angoli retti, cioè 180°; l'insetto
sulla sfera scoprirà invece che nei suoi triangoli la somma degli angoli è
sempre maggiore di 180°. Per triangoli piccoli, la differenza in eccesso è
piccola, ma essa cresce a mano a mano che i triangoli diventano più grandi e,
come caso limite, il nostro insetto sulla sfera sarà addirittura in grado di
disegnare triangoli con tre angoli retti. Infine, vediamo che cosa succede
quando i due insetti tracciano dei cerchi e ne misurano la circonferenza.
L'insetto sul piano troverà che la circonferenza è sempre uguale a 2 n volte il
raggio. indipendentemente dalle dimensioni del cerchio. L'insetto sulla sfera,
viceversa, noterà che la circonferenza è sempre minore di 2 t volte il raggio.
Come si può vedere nella figura qui sotto, il nostro punto di vista tridimensionale
ci permette di capire che quello che l'insetto considera il raggio del suo
cerchio è in effetti una curva che è sempre maggiore del raggio vero del
cerchio.
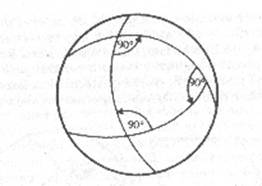
Su
una sfera un triangolo può avere tre angoli retti
Via via che i due insetti continuano a
studiare la geometria, quello sul piano scoprirà gli assiomi e le leggi della
geometria euclidea, ma il suo collega sulla sfera
scoprirà leggi diverse. La differenza sarà piccola per figure geometriche
piccole, ma aumenterà a mano a mano che le figure geometriche diventeranno più
grandi. L’esempio dei due insetti fa vedere che possiamo sempre determinare se
una superficie è curva oppure no semplicemente effettuando misurazioni
geometriche sulla superficie e confrontando i risultati con quelli previsti
dalla geometria euclidea. Se c’è una discrepanza, la
superficie è curva, e più grande è la discrepanza – per una data dimensione
della figura – maggiore è la curvatura.
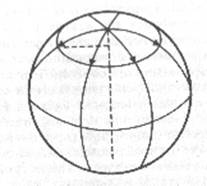
Come
si traccia una circonferenza su una sfera
Nello stesso modo, possiamo definire come spazio tridimensionale
curvo uno spazio nel quale non è più valida la geometria euclidea.
In esso, le leggi della geometria saranno di tipo diverso, «non euclideo». Una geometria non euclidea
di questo genere fu introdotta dal matematico Georg Riemann nel diciannovesimo secolo, come idea matematica
puramente astratta, e si ritenne che fosse niente di più che questo fino al
momento in cui Einstein propose la rivoluzionaria
ipotesi che lo spazio tridimensionale in cui viviamo è di fatto curvo. Secondo
la teoria di Einstein, la curvatura dello spazio è
prodotta dai campi gravitazionali dei corpi. Dovunque sia presente un oggetto
con massa, lo spazio circostante è curvo, e il grado di curvatura, vale a dire
il grado in cui la geometria devia da quella di Euclide, dipende dalla massa
dell'oggetto.
Le equazioni che mettono in relazione la curvatura dello spazio con
la distribuzione di materia presente in esso sono chiamate equazioni del campo
di Einstein. Possono essere applicate non solo per
determinare le variazioni locali di curvatura nelle vicinanze di stelle e
pianeti, ma anche per scoprire se c'è una curvatura globale dello spazio su
larga scala. In altre parole, le equazioni di Einstein
possono essere usate per determinare la struttura dell'universo nel suo
insieme. Purtroppo, esse non danno una risposta univoca, ma possono avere
soluzioni matematiche diverse; queste diverse soluzioni costituiscono i vari
modelli dell'universo studiati in cosmologia, alcuni dei quali verranno
esaminati nel prossimo capitolo. Determinare quale di essi corrisponda alla
struttura reale del nostro universo è il compito principale della cosmologia
dei nostri giorni.
Poiché nella teoria
della relatività lo spazio non può mai essere separato dal tempo, la curvatura
prodotta dalla gravità non può rimanere limitata allo spazio tridimensionale,
ma deve estendersi allo spazio-tempo quadridimensionale. E questo è, in effetti, quanto
prevede la teoria generale della relatività. In uno spazio-tempo curvo, le distorsioni
prodotte dalla curvatura riguardano non solo le relazioni spaziali descritte
dalla geometria, ma anche le durate degli intervalli di tempo. Il tempo non
scorre con la stessa rapidità che avrebbe nello «spazio-tempo piano», e col
variare della curvatura da punto a punto, in rapporto alla distribuzione della
massa dei corpi, varia corrispondentemente lo
scorrere del tempo. È importante rendersi conto, tuttavia, che questa
variazione dello scorrere del tempo può essere vista solo da un osservatore che
rimanga in un luogo diverso da quello degli orologi usati per misurare tale
variazione. Se l'osservatore, per esempio, si spostasse in un luogo nel quale
il tempo scorre più lentamente, anche tutti i suoi orologi rallenterebbero e
quindi egli non avrebbe alcun mezzo per misurare tale effetto.
Nel nostro ambiente terrestre, gli effetti della gravità sullo
spazio e sul tempo sono talmente piccoli da essere insignificanti, ma
nell'astrofisica, che tratta con corpi di grande massa, quali pianeti, stelle e
galassie, la curvatura dello spazio-tempo è un fenomeno importante. Finora
tutte le osservazioni hanno confermato la teoria di Einstein
e ci spingono quindi a credere che lo spazio-tempo sia di fatto curvo. Gli
effetti più drastici della curvatura dello spazio-tempo si manifestano durante
la contrazione - o «collasso» -
gravitazionale di una stella di grande massa. Secondo le idee correnti
dell'astrofisica, nel corso della sua evoluzione ogni stella raggiunge uno stadio
durante il quale essa si contrae a causa della mutua attrazione gravitazionale
tra le sue particelle. Poiché l'attrazione aumenta rapidamente col diminuire
della distanza tra le particelle, la contrazione accelera, e se la stella ha
una massa sufficientemente grande, pari a più di due volte quella del Sole,
nessun processo conosciuto può impedire che la contrazione prosegua
indefinitamente.
A mano a mano che la stella si contrae e diventa più densa, la
forza di gravità sulla sua superficie cresce sempre più, e di conseguenza
continua ad aumentare anche la curvatura dello spazio-tempo nella regione
circostante. A causa della crescente forza di gravità sulla superficie della
stella, diventa sempre più difficile allontanarsene, e alla fine la stella
raggiunge uno stadio in cui dalla sua superficie non può sfuggire nulla,
neanche la luce. A questo stadio diciamo che attorno alla stella si forma un
«orizzonte degli eventi», perché nessun segnale può allontanarsi da essa per
comunicare un evento qualsiasi al mondo esterno. Lo spazio attorno alla stella è quindi talmente curvo che tutta la
luce rimane confinata al suo interno e non può uscirne. Noi non siamo in grado
di vedere una stella di questo tipo, perché la sua luce non può mai
raggiungerci e per questo motivo la chiamiamo buco nero. L'esistenza dei
buchi neri fu prevista già nel 1916, sulla base della teoria della relatività;
recentemente l'argomento è stato posto al centro dell'attenzione dalla scoperta
di alcuni fenomeni stellari che sembrerebbero indicare l'esistenza di una
stella pesante che ruota attorno a una compagna invisibile, la quale potrebbe
essere un buco nero.
I buchi neri sono
tra gli oggetti più affascinanti e più misteriosi studiati dall'astrofisica
moderna e illustrano nel modo più spettacolare gli effetti della teoria della
relatività. La
forte curvatura dello spazio-tempo attorno ad essi non solo impedisce a tutta
la loro luce di raggiungerci, ma ha un effetto altrettanto impressionante sul
tempo. Se un orologio, che ci trasmette i suoi segnali, si trovasse sulla
superficie di una stella che si sta contraendo, noi osserveremmo che questi
segnali rallentano a mano a mano che la stella si approssima all'orizzonte
degli eventi finché, una volta che la stella fosse diventata un buco nero, non
ci giungerebbe più nessun segnale dall'orologio. Per un osservatore esterno, lo
scorrere del tempo sulla superficie della stella rallenta con la contrazione
della stella e si ferma del tutto all'orizzonte degli eventi. La contrazione
completa della stella avviene quindi in un tempo infinito. Tuttavia la stella
stessa non avverte nulla di particolare quando si contrae oltre l'orizzonte
degli eventi. Il tempo continua a scorrere normalmente e la contrazione è
completata dopo un periodo finito di tempo, quando la stella si è contratta in
un punto di densità infinita. Allora, quanto tempo occorre realmente per la
contrazione: un tempo finito o un tempo infinito? Nel mondo della teoria della
relatività, una domanda di questo tipo è priva di senso. La durata della vita
di una stella che si contrae, come tutti gli altri intervalli di tempo, è
relativa e dipende dal sistema di riferimento dell'osservatore.
Nella teoria generale della relatività, i concetti classici di
spazio e di tempo come entità assolute e indipendenti sono totalmente aboliti.
Non solo sono relative tutte le misurazioni riguardanti lo spazio e il tempo,
poiché dipendono dallo stato di moto dell'osservatore, ma l'intera struttura
dello spazio-tempo è inestricabilmente legata alla distribuzione della materia.
Lo spazio è curvo in misura diversa e il
tempo scorre diversamente in punti diversi dell'universo. Siamo quindi
giunti a comprendere che le idee di spazio euclideo
tridimensionale e di tempo che scorre linearmente sono limitate alla nostra
esperienza ordinaria del mondo fisico e devono essere completamente abbandonate
quando ampliamo questa esperienza.
Anche i saggi orientali
parlano di ampliamento della loro esperienza del mondo durante gli stati
superiori di coscienza, e affermano che questi stati comportano un'esperienza
totalmente diversa dello spazio e del tempo. Essi insistono sul fatto che non
solo, durante la meditazione, vanno al di là dell'ordinario spazio
tridimensionale, ma anche - e sottolineano questo con vigore ancora maggiore
- trascendono
l'ordinaria consapevolezza del tempo. Invece di una successione lineare di
istanti, essi percepiscono - così dicono - un presente infinito, eterno, e
tuttavia dinamico. Nelle seguenti citazioni, tre mistici orientali - il saggio taoista Chuang-tzu, il sesto
patriarca Zen Hui- neng e
lo studioso contemporaneo di Buddhismo D.T. Suzuki - parlano dell'esperienza di questo «eterno
presente»:
«Dimentichiamo il trascorrere del tempo; dimentichiamo i contrasti
di opinioni. Facciamoci assorbire dall'infinito e occupiamo in esso il nostro
posto».
«L'assoluta tranquillità è il momento presente. Sebbene sia in
questo momento, questo momento non ha limiti, e quivi è eterno diletto».
«In questo mondo spirituale non ci sono suddivisioni di tempo come
passato, presente e futuro; esse si sono contratte in un singolo istante del
presente nel quale la vita freme nel suo vero senso... Il passato e il futuro
sono entrambi racchiusi in questo momento presente di illuminazione e questo
momento presente non è qualcosa che sta in quiete con tutto ciò che contiene,
ma si muove incessantemente».
È quasi impossibile parlare dell'esperienza di eterno presente,
perché tutte le parole come «eterno», «presente», «passato», «istante», ecc.,
si riferiscono all'idea convenzionale di tempo. È quindi estremamente difficile
comprendere cosa vogliano dire i mistici in passi come quelli citati; ma qui,
di nuovo, la fisica moderna può facilitare la comprensione, in quanto può
essere usata per illustrare con esempi grafici come le sue teorie trascendano
le nozioni ordinarie di tempo.
Nella fisica relativistica, la storia di un oggetto, per esempio di
una particella, può essere rappresentata in un cosiddetto «diagramma
spazio-tempo» (si veda figura a p. 210).
In questi diagrammi, la direzione orizzontale rappresenta lo spazio, e la direzione
verticale il tempo. (1)
(1). In questi diagrammi, lo spazio ha una sola dimensione; le
altre due dimensioni sono state eliminate per poter disegnare il diagramma su
un piano
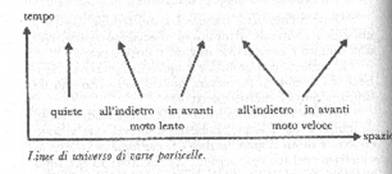
Linee
di universo di varie particelle
La traiettoria della particella nello spazio-tempo si chiama la sua
«linea
di universo». Anche quando è in quiete, la particella si muove nel
tempo e in tal caso la sua «linea di universo» è una retta
verticale. Se la particella si muove nello spazio, la sua linea di universo
sarà inclinata, con un'inclinazione tanto maggiore quanto più grande è la
velocità della particella. Si noti che le particelle possono muoversi solo in
avanti nel tempo, ma sia in avanti che indietro nello spazio. Le loro linee di
universo possono avere inclinazioni diverse rispetto all'orizzontale, ma non
possono mai diventare perfettamente orizzontali, poiché ciò significherebbe che
una particella viaggia da un punto all'altro in un tempo nullo.
I diagrammi spazio-tempo sono usati nella fisica relativistica per
rappresentare le interazioni tra varie particelle. Per ciascun processo,
possiamo tracciare un diagramma e associare ad esso una espressione matematica
definita che ci dà la probabilità che si verifichi il processo. Per esempio,
l'urto, o «diffusione», tra un elettrone e un fotone può essere rappresentato
con il seguente diagramma. Questo diagramma dev'essere
letto nel seguente modo (a cominciare dal basso verso l'alto, secondo la
direzione del tempo): un elettrone (indicato con e- poiché ha carica negativa)
urta un fotone (indicato con y); il fotone è assorbito dall'elettrone che
continua la sua traiettoria con velocità diversa (e di conseguenza varia la
pendenza della linea di universo); dopo un certo tempo l'elettrone emette
nuovamente il fotone e inverte la sua direzione di moto.
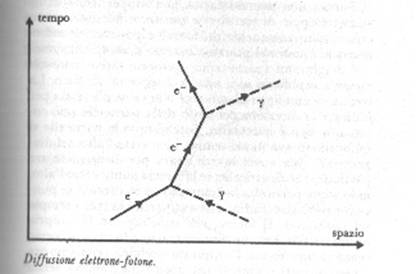
Diffusione
elettrone-fotone
La teoria che fornisce lo schema interpretativo adeguato per questi
diagrammi spazio-tempo e per le espressioni matematiche a essi associate si
chiama « teoria dei campi ». Si tratta di una delle più importanti teorie
relativistiche della fisica moderna, i cui concetti fondamentali saranno
esaminati più avanti. Per la nostra discussione dei diagrammi spazio-tempo,
sarà sufficiente conoscere due aspetti particolari di questa teoria. Il primo è
il fatto che tutte le interazioni comportano la creazione e la distruzione di
particelle, come l'assorbimento e l'emissione del fotone nel nostro diagramma;
il secondo aspetto è la simmetria di fondo che esiste tra particelle e
antiparticelle. Per ogni particella, esiste un'antiparticella con massa uguale
e carica opposta. L'antiparticella dell'elettrone, per esempio, viene chiamata
positrone e in genere è indicata col simbolo e+. Il
fotone, non avendo carica, è l'antiparticella di se stesso. Coppie di elettroni
e positroni possono essere create spontaneamente da fotoni e possono
ritrasformarsi in fotoni nel processo inverso di annichilazione.
I diagrammi spazio-tempo possono essere notevolmente semplificati
se si adotta il seguente artificio. La freccia su una linea di universo non
viene più usata per indicare la direzione del moto della particella (ciò
comunque non è necessario, poiché tutte le particelle si muovono in avanti nel
tempo, cioè verso l'alto nel diagramma), ma viene invece usata per distinguere
tra particelle e antiparticelle: se la freccia punta verso l'alto, indica una
particella (ad esempio un elettrone), se punta verso il basso, indica una
antiparticella (per esempio un positrone). Il fotone, che coincide con la
propria antiparticella, è rappresentato con una linea di universo senza alcuna
freccia. Con questa modifica, possiamo ora omettere tutti i simboli nel nostro
diagramma senza provocare alcuna confusione: le linee con frecce rappresentano
elettroni, quelle senza frecce fotoni. Per rendere il diagramma ancora più
semplice, possiamo anche omettere gli assi dello spazio e del tempo, ricordando
che la direzione del tempo va dal basso verso l'alto e che la direzione in
avanti nello spazio va da sinistra a destra.
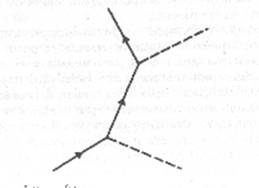
Diffusione
elettrone-fotone
Con queste semplificazioni, il diagramma spazio-tempo per la
diffusione elettrone-fotone avrà l'aspetto della figura precedente. Se vogliamo
invece rappresentare un processo di diffusione tra un fotone e un positrone,
possiamo tracciare lo stesso diagramma e invertire sem-
plicemente la direzione delle frecce, come nella
figura seguente:
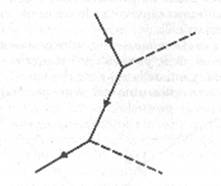
Diffusione
elettrone-fotone
Finora, non c'è stato nulla di insolito nella nostra discussione
sui diagrammi spazio-tempo. Li abbiamo letti dal basso verso l'alto, secondo la
nostra idea convenzionale di tempo che scorre linearmente. L'aspetto insolito
si trova nei diagrammi che contengono linee di positroni, come in quello che
rappresenta una diffusione positrone-fotone. Il formalismo matematico della
teoria dei campi suggerisce che queste linee possono essere interpretate in due
modi: o come positroni che si muovono in avanti nel tempo, o come elettroni che
si muovono all'indietro nel tempo! Dal punto di vista matematico, le due
interpretazioni sono identiche; la stessa espressione descrive una
antiparticella che si muove dal passato verso il futuro, oppure una particella
che si muove dal futuro verso il passato. Possiamo quindi vedere i nostri due
diagrammi come rappresentazioni dello stesso processo che si evolve in
direzioni diverse nel tempo. Entrambi possono essere interpretati come
diffusione di elettroni e fotoni, ma in un processo le particelle si muovono in
avanti nel tempo, nell'altro si muovono all'indietro. (1).
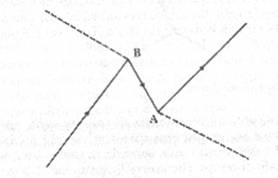
Processo
di diffusione al quale prendono parte fotoni, elettroni e un positrone
La teoria relativistica
delle interazioni tra particelle presenta quindi una perfetta simmetria
rispetto alla direzione del tempo. Tutti i diagrammi spazio-tempo possono
essere letti in entrambe le direzioni. Per ogni processo, esiste un processo
equivalente in cui la direzione del tempo è invertita e le particelle sono
sostituite da antiparticelle.2
Per vedere in che modo questa sconcertante caratteristica del mondo
delle particelle subatomiche influenza le nostre concezioni dello spazio e del
tempo, consideriamo il processo illustrato nel seguente diagramma:
Leggendo il diagramma nel modo convenzionale, dal basso verso
l'alto, lo possiamo interpretare come segue: un elettrone (rappresentato da una
linea a tratto continuo) e un fotone (rappresentato da una linea tratteggiata)
si avvicinano l'uno all'altro; nel punto A il fotone crea una coppia
elettrone-positrone, l'elettrone si allontana rapidamente verso destra, il
positrone verso sinistra; il positrone e l'elettrone iniziale entrano quindi in
collisione nel punto B, si annichilano l'uno con l'altro e durante questo
processo creano un fotone che si allontana rapidamente verso sinistra. In
alternativa, possiamo anche interpretare il processo come l'interazione di due
fotoni con un singolo elettrone che prima si sposta in avanti nel tempi, quindi
all'indietro e poi nuovamente in avanti. Per questa interpretazione, seguiamo
semplicemente le frecce sulla linea di universo dell'elettrone per tutto il suo
percorso; l'elettrone si sposta verso il punto B dove emette un fotone e
inverte la sua direzione, per viaggiare all'indietro nel tempo fino al punto A;
qui assorbe il fotone iniziale, inverte nuovamente la sua direzione e si
allontana rapidamente in avanti nel tempo. In un certo senso, la seconda
interpretazione è molto più semplice, perché seguiamo soltanto la linea di
universo di una particella. D'altra parte, notiamo immediatamente che così
facendo incorriamo in serie difficoltà di linguaggio. L'elettrone viaggia
«prima» verso il punto B e «poi» verso il punto A; eppure l'assorbimento del
fotone in A avviene prima dell'emissione dell'altro fotone in B.
Il modo migliore per evitare queste difficoltà è di vedere
diagrammi spazio-tempo di questo genere non come registrazioni cronologiche
delle traiettorie delle particelle nel tempo, ma piuttosto come figure
quadri-dimensionali nello spazio-tempo, che rappresentano una rete di eventi
interconnessi, ai quali non va attribuita alcuna direzione definita del tempo.
Poiché tutte le particelle possono muoversi in avanti e all'indietro nel tempo,
proprio come possono muoversi a destra e a sinistra nello spazio, non ha alcun
senso imporre sui diagrammi un flusso unidirezionale del tempo. Essi sono
semplicemente mappe quadridimensionali tracciate nello spazio- tempo in modo
tale che non possiamo parlare di sequenze temporali.
Per usare le parole di Louis de Broglie:
«Nello spazio-tempo, tutto ciò che per ciascuno di noi costituisce
il passato, il presente e il futuro è dato in blocco... Ciascun osservatore col
passare del suo tempo scopre, per così dire, nuove porzioni dello spazio-tempo,
che gli appaiono come aspetti successivi del mondo materiale, sebbene in realtà
l'insieme degli eventi che costituiscono lo spazio-tempo esistesse già prima di
essere conosciuto .
Questo, quindi, è il pieno significato dello spazio-tempo nella
fisica relativistica. Spazio e tempo sono del tutto equivalenti, essi sono
unificati in un continuo quadridimensionale nel quale le interazioni tra le
particelle possono estendersi in qualsiasi direzione. Se vogliamo raffigurare
queste interazioni, dobbiamo rappresentarle in una « istantanea
quadridimensionale » che copra l'intero intervallo di tempo come pure l'intera
regione di spazio. Per ottenere la sensazione esatta del mondo relativistico
delle particelle, dobbiamo «dimenticare il trascorrere del tempo», come dice Chuang-tzu; ed è per questo che i diagrammi spazio-tempo
della teoria dei campi possono essere un'analogia utile per capire l'esperienza
dello spazio-tempo dei mistici orientali. La pertinenza dell'analogia è resa
evidente dalle seguenti considerazioni del Lama Govinda
a proposito della meditazione buddhista:
« ... Se parliamo dell'esperienza spaziale ottenuta nella
meditazione, abbiamo a che fare con una dimensione del tutto diversa... In
questa esperienza spaziale, la successione temporale è trasformata in una
simultanea coesistenza, l'esistenza parallela delle cose..., e anche questa non
rimane statica, ma diventa un continuum vivente in cui tempo e spazio sono
integrati... ».
Sebbene i fisici usino il loro formalismo matematico e i loro
diagrammi per rappresentare «in blocco» le interazioni nello spazio-tempo
quadridimensionale, essi dicono che nel mondo reale ogni osservatore può fare
esperienza dei fenomeni solo in una successione di sezioni dello spazio-tempo,
cioè in una sequenza temporale. I mistici, viceversa, sostengono di poter
realmente percepire la pienezza di un intervallo dello spazio-tempo nel quale
il tempo non fluisce più. Ad esempio, Dogen, un
maestro Zen, dice:
«La maggior parte delle persone crede che il tempo trascorra; in
realtà esso sta sempre là dov'è. Questa idea del trascorrere può essere
chiamata tempo, ma è un'idea inesatta; infatti, dato che lo si può vedere solo
come un trascorrere, non si può comprendere che esso sta proprio dov'è».
Molti dei maestri orientali mettono in rilievo che il pensiero deve
svolgersi nel tempo, ma che l'intuito può trascenderlo. «L'intuito» dice Govinda «è legato allo spazio di una dimensione superiore
ed è, quindi, senza tempo». Lo spazio-tempo della fisica relativistica è anch'esso
uno spazio privo di tempo, che appartiene a una dimensione superiore. In esso,
tutti gli eventi sono interconnessi, ma le connessioni non sono causali. Le
interazioni tra particelle possono essere interpretate in termini di causa ed
effetto solo quando i diagrammi spazio-tempo sono letti in una determinata
direzione, per esempio dal basso verso l'alto. Quando vengono considerati come
figure quadridimensionali prive di una direzione definita del tempo, non c'è un
«prima» né un «dopo», e quindi nessuna relazione di causalità.
In maniera analoga, i mistici orientali affermano che nel
trascendere il tempo essi trascendono anche il mondo della causa e
dell'effetto. Come le nostre ordinarie nozioni di spazio e tempo, la causalità
è un'idea limitata a una certa esperienza del mondo e deve essere abbandonata
quando questa esperienza viene ampliata. Così si esprime Swami
Vivekananda:
«Tempo, spazio e causalità sono la lente attraverso la quale si
vede l'Assoluto ... Nell'Assoluto in se stesso non ci sono né tempo, né spazio,
né causalità».
Le tradizioni spirituali orientali indicano ai loro seguaci vari
modi per andare al di là dell'ordinaria esperienza del tempo e per liberarsi
dalla catena di causa ed effetto: dal vincolo delk a
r m a n, come dicono gli Indù e i Buddhisti. Perciò è
stato detto che il misticismo orientale è una liberazione dal tempo. In un
certo senso, la stessa cosa si può dire della fisica relativistica.
|
|
Altri argomenti
del Tao
© www.mimmademaio.com - 2012
|
|